正二十面体的展开图

二十面体是由20个等边三角形组成的正多面体，有12个顶点，30条边和20个面。

它是五个柏拉图多面体之一。所有的面都是全等的正多边形，所有的多边形角都是全等的多边形角。其中正四面体的面数最少。
正二十面体的顶点能共同分成五组，每组拥有三个同心、相互垂直的黄金矩形。 在直角坐标系中，一个边长为二、重心在圆点的正二十面体的坐标分别为： 其中 φ = 1 + √ 5 / 2 是黄金比例（或记为 τ ）。值得注意的是，这些顶点能共同形成五组，每组拥有三个同心、相互垂直的黄金矩形，其边形成 博罗梅安环 （ 英语 ： Borromean rings ） ，其中，前者是因为正二十面体与黄金比例有密切的关系。 如果原始的二十面体的边长为1，那么它的对偶——正十二面体的边长就是 √ 5 − 1 / 2 ，正好是一个黄金比例。

从心脏到每个顶点的距离(外切球的半径)= 从心脏到每个面的中心的距离(内接球体半径)= 从主体中心到每条边的中点的距离(切削刃球体的半径)= 扩展数据 自然：
1.正二十面体的外切球、内接球和内接球都存在，三个球的中心重合。

2.二十面体的外中心、内中心和内边中心重合的点称为二十面体的中心。

3.通过正二十面体任一顶点和正多面体中心的直线必通过正二十面体的另一顶点，这两个顶点到正二十面体中心的距离相等。

4.连接通过二十面体中心的直线的两点称为相对顶点，连接两对相对顶点的两条边称为二十面体的对边，被对边包围的两个面称为二十面体的对边。

5.二十面体的对边和面是平行的。

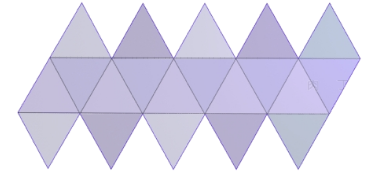
正二十面体折纸
折纸给大多数人的印象看似没门槛，做起来却好难，所以折纸这项艺术运动一直都比较小众。希望更多的人能耐心来学习下折纸，折纸不仅仅能锻炼你的耐心，更能帮助孩子更好的学习数学。

今天给大家分享的几何体折纸：正二十面体，看似很难，其实没有什么难度。这篇文章树姐姐还带大家一起回忆下之前1号花球的做法花球折纸：20个圆形制作花球的方法，大家做完后对比下它们有什么不同吧？

所需材料：同等直径圆形20个，白胶，圆规，简单，尺子，笔。

图1、将正方形2条对角线对折形成的交叉点O。以0为圆心，取任意半径在正方形内画圆；

取任意直径标出A、B两点，以A为圆心，OA为半径画弧，交于圆上C、D两点，如上图1所示。

图2、将BC、CD、BD相连，就形成了圆内的正三边形。这三条线可画也可不画，对于折直线比较困难的小朋友，建议把直线画出来。

图3、将圆弧向中心点平行对折，如上图所示。

图4、我们将图3翻过来，你会发现中间正好是一个正三边形。

图5、20个组件同样的制作方法，粘之前，建议大家给每个组件标行数字，这样在组装的时候会更清晰。

图6、将1-5、6-10号组件分别粘成2个盖子一样的形状，如上图所示。

图7、将11-20号组件粘成一个长条，注意看下上图组件的摆放，粘的时候别错了。

图8、图7固定好之后，将首尾固定成圈，然后将1-5、6-10号组件分别固定于11-20号组件的两边，这样正二十面体和1号花球就做好了。

图9-1号花球

---

 正二十面体的面邻接图，就相当于其对偶（正十二面体）的顶点图：

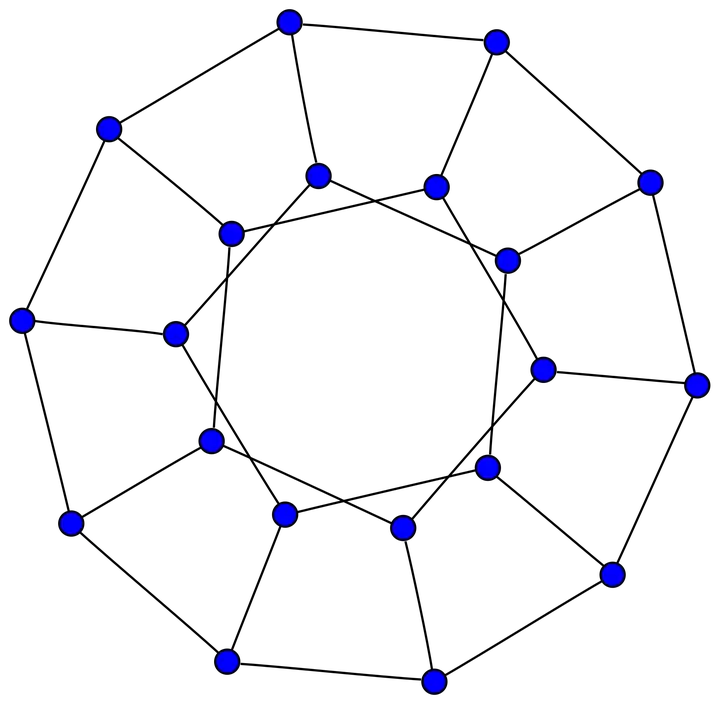
然后只要找出这个图里所有的生成树，这本身很简单，利用Kirchhoff定理只要找出邻接矩阵的特征值就可以算了。

可得生成树总数为 120(3−5)3(3+5)3255434=293453=5184000

问题在于结构相同的展开不能重复计算。

这里就涉及上图的自同构性质，换句话说，找到上图顶点集合到自身的映射。显然，因为自同构不改变顶点相邻的性质，任何生成树在自同构下依然是生成树。

举个例子，下图左边是立方体的两种等价的展开方式，在右边的面邻接图上对应两棵不同的生成树，但是在自同构下第一棵生成树会被映射到第二棵。

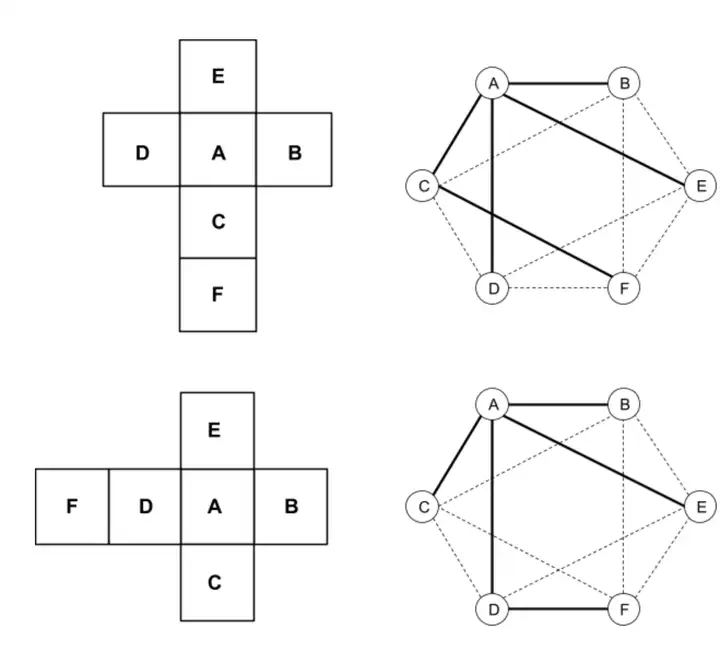
根据群论已知十二面体图的自同构数目为120（5阶交错群和2阶循坏群的乘积），所以答案就是 518400/120=43200 ？

可惜没那么简单，以上假设每棵对应不同展开的生成树都会被120种自同构变成120棵不同的生成树，加起来总共有518400棵。但实际上某些自同构会把某些生成树映射到自己本身，518400里面不包括这些重复的生成树。

事实上，大部分自同构都无法将任何生成树映射到自身，文中讨论了能够将至少一棵生成树映射到自身的自同构，发现所有这些自同构都是二阶，而且没有不动点。由此得到所有这些自同构都是围绕两条对边的转动，所以一共有15种，每种转动下不变的生成树共有1440棵。

因此答案为 1120(518400+15×1440)=43380